Recipe2cuisine
Recipe2cuisine: Part1
In this post I want to share my experience with an Natural Language Processing (NLP) data challenge I tackled at Insight Data Science.
The Goal
Imagibe that you’ve just joined the data team at an online publishing company. One of your verticals is a food publication. A product manager on your team wants to build a feature for this vertical that enables users to query by cuisine, not just by ingredients. Most of your recipes are unlabeled, and it’s infeasible to label them by hand. Luckily, you have a small-ish training set of about 30,000 recipes with labeled cuisines. Design and execute a method to predict the cuisine of a recipe given only its ingredients. For each each major cuisine, what are the driving ingredients that characterize it?
Approach
As always with any data science problem, I have to explore the data, and learn what type of data cleaning/wrangling would be necesary. Our labeled training data looks like this:
[
{
"id": 10259,
"cuisine": "greek",
"ingredients": [
"romaine lettuce",
"black olives",
"grape tomatoes",
"garlic",
"pepper",
"purple onion",
"seasoning",
"garbanzo beans",
"feta cheese crumbles"
]
},
{
"id": 25693,
"cuisine": "southern_us",
"ingredients": [
"plain flour",
"ground pepper",
"salt",
"tomatoes",
"ground black pepper",
"thyme",
"eggs",
"green tomatoes",
"yellow corn meal",
"milk",
"vegetable oil"
]
}
That is, a json file with a labelled cuisine followed by the ingredients of each recipe. Using pandas and matplotlib, we can plot the number of recipes per cuisine:
%matplotlib inline
import numpy as np
import pandas as pd
from sklearn.feature_extraction.text import TfidfTransformer, CountVectorizer, TfidfVectorizer
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from nltk.stem import WordNetLemmatizer
from nltk import word_tokenize
from sklearn.naive_bayes import MultinomialNB, ComplementNB
from sklearn.pipeline import Pipeline
from sklearn.model_selection import cross_validate
from sklearn import metrics
from sklearn.decomposition import PCA
plt.style.use('ggplot')
filename = '../Challenge_Recipe2Cuisine/recipies.json'
recipes = pd.read_json(filename)
print('Minimum number of ingredients:', recipes.ingredients.apply(lambda x: len(x)).min())
print('Maximum number of ingredients:', recipes.ingredients.apply(lambda x: len(x)).max())
print('Number of cuisines:', recipes.cuisine.unique().shape[0])
recipes.groupby('cuisine').count()['id'].plot(kind='bar')
Minimum number of ingredients: 1
Maximum number of ingredients: 65
Number of cuisines: 20
<matplotlib.axes._subplots.AxesSubplot at 0x11ca156d0>
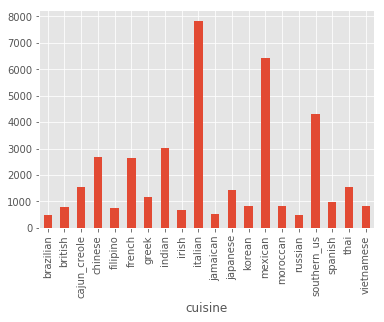
I see that we have a significant class imbalance towards Italian and Mexican cuisine. Also note that 1 ingredient is hardly a recipe, and 65 might be a bit excessive, so let’s plot the distribution of number of ingredients, and let’s print some samples from the extremes:
recipes['n_ingredients'] = recipes.ingredients.apply(lambda x: len(x))
print('Single ingredient\n', recipes[recipes.n_ingredients == 1].head())
print('\nLots of ingredients\n', recipes[recipes.n_ingredients == 65].ingredients.tolist()[0])
recipes.n_ingredients.hist(bins=50)
Single ingredient
cuisine id ingredients n_ingredients
940 japanese 4734 [sushi rice] 1
2088 vietnamese 7833 [dried rice noodles] 1
6787 indian 36818 [plain low-fat yogurt] 1
7011 indian 19772 [unsalted butter] 1
8181 japanese 16116 [udon] 1
Lots of ingredients
['fettucine', 'fresh marjoram', 'minced garlic', 'olive oil', 'garlic powder', 'large eggs', 'Alfredo sauce', 'vegetable oil', 'cajun seasoning', 'shredded romano cheese', 'basil dried leaves', 'salt', 'cayenne pepper', 'scallions', 'red bell pepper', 'boneless skinless chicken breast halves', 'soba', 'pasta sauce', 'kosher salt', 'milk', 'fresh ginger', 'ground black pepper', 'flour', 'cooked chicken', 'coarse salt', 'lemon', 'diced tomatoes', 'garlic', 'rice vinegar', 'Neufchâtel', 'garlic cloves', 'dried parsley', 'frozen artichoke hearts', 'penne', 'pepper', 'sweet onion', 'part-skim mozzarella cheese', 'parmigiano reggiano cheese', 'basil leaves', 'onion powder', 'red wine vinegar', 'red pepper flakes', 'orzo', 'crushed red pepper', 'all-purpose flour', 'freshly ground pepper', 'sliced mushrooms', 'panko breadcrumbs', 'plum tomatoes', 'fresh basil', 'fresh leav spinach', 'water', 'sun-dried tomatoes', 'ground pepper', 'grated parmesan cheese', 'boneless skinless chicken breasts', 'chicken cutlets', 'butter', 'multi-grain penne pasta', 'extra-virgin olive oil', 'cilantro leaves', 'green pepper', 'shredded mozzarella cheese', 'fresh parsley', 'spaghetti']
<matplotlib.axes._subplots.AxesSubplot at 0x1241415d0>
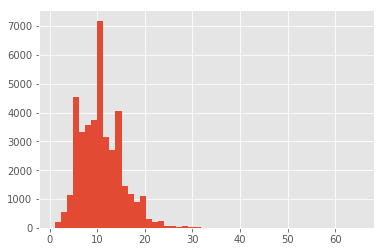
Definitively we have issues with these two classes. Sushi rice, for example, is not a recipe but an ingredient. The second class, contains multiple types of pasta, different sauces, repeated ingredients. This lead me to believe that some recipes have been mistakenly merged, and we need to get rid of such noise. Now focusinng our attention to the histogram, we can see that we have a long tail of low frequency ingredients, most likely composed of those mistakes we already saw. Let’s remove the extreme outside of the 95% confidence through percentiles and reassess:
low = np.quantile(recipes.n_ingredients, 0.05)
high = np.quantile(recipes.n_ingredients, 0.95)
print('Low percentile:', low)
print('High percentile:', high)
sub = recipes[(recipes.n_ingredients >= low) & (recipes.n_ingredients <= high)].copy(deep=True)
max_ing = sub.n_ingredients.max()
min_ing = sub.n_ingredients.min()
print('\nLots of ingredients\n', recipes[recipes.n_ingredients == max_ing].ingredients.tolist()[0])
print('\nFew of ingredients\n', recipes[recipes.n_ingredients == min_ing].ingredients.tolist()[0])
print('\nNumber of recipes after filter:', sub.shape[0])
sub.n_ingredients.hist(bins=15)
Low percentile: 5.0
High percentile: 19.0
Lots of ingredients
['black beans', 'olive oil', 'chili powder', 'tortilla chips', 'cheddar cheese', 'store bought low sodium chicken stock', 'chipotle', 'cilantro leaves', 'dried oregano', 'avocado', 'kosher salt', 'ground black pepper', 'garlic', 'sour cream', 'ground chicken', 'cherry tomatoes', 'jalapeno chilies', 'cayenne pepper', 'ground cumin']
Few of ingredients
['yellow corn meal', 'boiling water', 'butter', 'fresh parmesan cheese', 'sea salt']
Number of recipes after filter: 36374
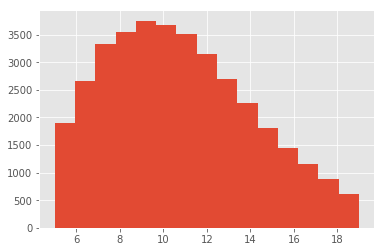
We can see that despite stll having a tail, both the longer and the sorter recipes can be related to actual dishes. In this case it seems that the longer list includes some sort of nachos, and the shorter list, a polenta-like recipe. As you probably already notice, there are a few confounders in the ingredients:
- Extrenious words such as
store bought, and brand names - Extra words that might be important for the recipe, but not for classification, such as shredded cheese as opposed to just cheese.
For this post I am going to ignore this and try to classify with the ingredients as they are, and see how we do. In subsequent posts I’ll explain how to deal with such data.
We have, however, seen how imbalance our dataset is. Let’s take a look of what happened after cleaning:
sub.groupby('cuisine').count()['id'].plot(kind='bar')
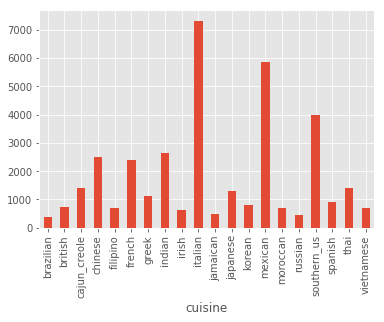
As you can see the imbalance remained. Here I will try first to ignore such an imbalance, but will later revise the model. Since we know that there were mistakes made (e.g. multiple recipes in one), let’s check if there is any mistakes in the ingredients. One way to do this is to plot their lengths and print some of the longer and shorter ones:
sub['min_ingredient_length'] = sub.ingredients.apply(lambda x: min([len(y) for y in x]))
sub['short_ingredient'] = sub.ingredients.apply(lambda x: [y for y in x if len(y) <= min([len(z) for z in x])])
sub['max_ingredient_length'] = sub.ingredients.apply(lambda x: max([len(y) for y in x]))
sub['long_ingredient'] = sub.ingredients.apply(lambda x: [y for y in x if len(y) >= max([len(z) for z in x])])
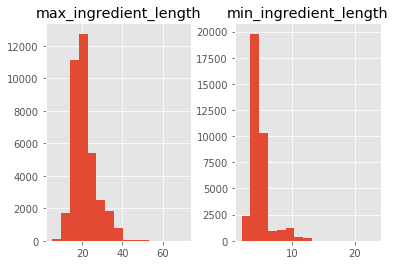
print('Maximum ingredient lenght', sub.max_ingredient_length.max())
print('Minimum ingredient lenght', sub.min_ingredient_length.min())
sub.loc[:, ['max_ingredient_length', 'min_ingredient_length']].hist(bins=15)
Maximum ingredient lenght 71
Minimum ingredient lenght 2
print(sub[sub.max_ingredient_length > 65].loc[:, 'long_ingredient'])
print(sub[sub.max_ingredient_length == 71].loc[:, 'long_ingredient'].tolist()[0][0])
283 [bertolli vineyard premium collect marinara wi...
10566 [bertolli vineyard premium collect marinara wi...
14118 [bertolli vineyard premium collect marinara wi...
16156 [bertolli vineyard premium collect marinara wi...
22313 [Pillsbury™ Crescent Recipe Creations® refrige...
26373 [KRAFT Mexican Style Shredded Four Cheese with...
37248 [bertolli vineyard premium collect marinara wi...
Name: long_ingredient, dtype: object
Pillsbury™ Crescent Recipe Creations® refrigerated seamless dough sheet
It seems that even the very long ingredients are not mistakes, but
contain many brands. As mentioned before that is a problem for another
post. For now, let’s see if we can solved the classification problem
linearly. To do this, we can explore our data with PCA, but we first
need to tranfor the lists of ingredients into a numerical series. Let’s
star with bag of words (BOW) using scikitlearn CountVectorizer.
By default, this class will tokenize and pre-process our ingredients by
word. As we mentioned before, we do not want that, since it is already
tokenized. We therefore need to create a dummy tokenizer and a dummy
pre-processing class class, and then create the BOW. However, because
eventually we would like to differentiate among classes, we would like
to normalized by document. This is done through TF-IDF transformation,
since is intended to reflect how important a word is to a document,
which will help us also to determine the most representative ingredients
in each cuisine:
import re
class Dummy_Tokenizer(object):
def __init__(self):
pass
def __call__(self, doc):
# make sure document is a list of lists
assert isinstance(doc, list)
return doc
class Dummy_Preprocessor(object):
def deaccent(self, string):
#remove accents
string = string.encode(encoding='ascii',errors='ignore').decode('ascii')
# also remove things between parenthesis (normally quantities)
return re.sub("[\(\[].*?[\)\]]", "", string.lower())
def __call__(self, doc):
assert isinstance(doc, list)
return [self.deaccent(x) for x in doc]
vect = CountVectorizer(tokenizer=Dummy_Tokenizer(), preprocessor=Dummy_Preprocessor())
doc = sub.ingredients.tolist()
BOW = vect.fit_transform(doc)
tf_idf = TfidfTransformer().fit_transform(BOW)
# lets make it a dense matrix in pandas (PCA will require this anyhow)
normalized_bow = pd.DataFrame(tf_idf.toarray(), index=sub.cuisine, columns=vect.get_feature_names())
print(normalized_bow.shape)
normalized_bow.head()
(36374, 6475)
| diced tomatoes | frozen chopped spinach | frozen chopped spinach, thawed and squeezed dry | refried beans | sweetened condensed milk | tomato paste | tomato sauce | 1% low-fat buttermilk | 1% low-fat chocolate milk | 1% low-fat cottage cheese | ... | yuzukosho | za'atar | zatarains creole seasoning | zatarains jambalaya mix | zest | zesty italian dressing | zinfandel | ziti | zucchini | zucchini blossoms | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| cuisine | |||||||||||||||||||||
| greek | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| southern_us | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| filipino | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| jamaican | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| spanish | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
5 rows × 6475 columns
With this matrix representation, we can more easily explore how common a given ingredient is. But why would we do that? We want to remove noise from our data, that means ingredients that are too frequent (most cuisines have it) and ones that are only used in a few recipes, can confound the predictions:
ingredients_usage = (normalized_bow > 0).sum(axis=0)
print('Sample of ingredients uses once:\n', ingredients_usage[ingredients_usage == 1].head(), '\n')
print('Sample of ingredients used in at least 10K recipes:\n', ingredients_usage[ingredients_usage > 10000].head(), '\n')
print('Distribution of values:\n', ingredients_usage.describe(), '\n')
low = (ingredients_usage > ingredients_usage.min())
high = (ingredients_usage < ingredients_usage.max())
print('Distribution of values without extremes\n', ingredients_usage[low & high].describe(), '\n')
ingredients_usage.hist(bins=100)
Sample of ingredients uses once:
2% low fat cheddar chees 1
2% milk shredded mozzarella cheese 1
33% less sodium cooked deli ham 1
33% less sodium cooked ham 1
33% less sodium smoked fully cooked ham 1
dtype: int64
Sample of ingredients used in at least 10K recipes:
salt 16856
dtype: int64
Distribution of values:
count 6475.000000
mean 59.921236
std 364.165886
min 1.000000
25% 1.000000
50% 4.000000
75% 19.000000
max 16856.000000
dtype: float64
Distribution of values without extremes
count 4756.000000
mean 77.673675
std 345.920981
min 2.000000
25% 3.000000
50% 9.000000
75% 34.000000
max 7432.000000
dtype: float64
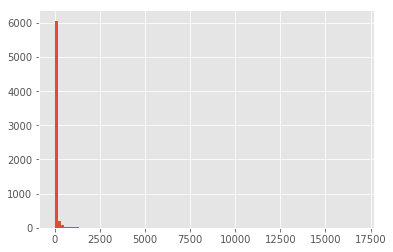
We can see that there are a lot of ingredients that are used only in one recipe, and there are a few used in all recipes (e.g. Salt). For the sake of simplicity, I would remove any ingredient that is use in less than 9 recipes (median of the distribution of values without extremes), and more than 7432 (max value without extremes):
low = (ingredients_usage >= 9)
high = (ingredients_usage <= 7432)
reduced_bow = normalized_bow.loc[:, (low & high)]
print('New shape:', reduced_bow.shape)
ingredients_usage[low & high].hist(bins=100)
New shape: (36374, 2405)
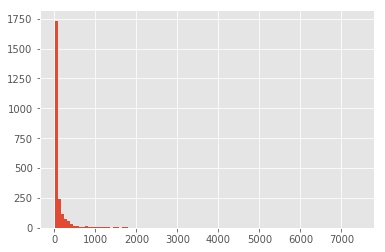
With a somewhat cleaner BOW, we can check how it looks in the first two Principal Components:
cuisines = set(reduced_bow.index)
n_cuisines = len(cuisines)
all_colors = np.linspace(0,len(plt.get_cmap('viridis').colors), n_cuisines, dtype=int)
colors = dict(zip(cuisines, all_colors))
c = [colors[x] for x in reduced_bow.index]
pca = PCA(n_components=2)
pca_mat = pca.fit_transform(reduced_bow)
plt.scatter(pca_mat[:,0], pca_mat[:,1], c=c, cmap='viridis')
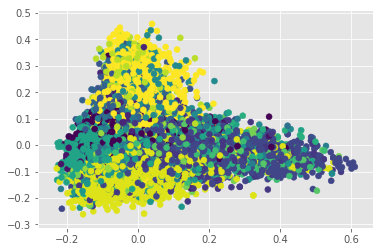
Apparently our problem does not seem to be linear. Let’s confirm this doing an LDA. This step works as a conformation since LDA maximizes the distances between classes, and in doing so, overfits. If a set is not separable by LDA, there is a high likelihood that this problem cannot be solve linearly:
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
lda = LDA(n_components=2)
lda_mat = lda.fit_transform(reduced_bow, reduced_bow.index)
plt.scatter(lda_mat[:,0], lda_mat[:,1], c=c, cmap='viridis')
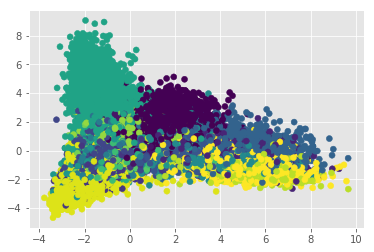
This confirms our suspicions, so we need a more complex model to deal with this classification problem, but before we delve into it, let’s see what are the most representative ingredents per cuisine. We can leverage the TF-IDF normalization since by definition it is “a numerical statistic that is intended to reflect how important a word is to a document in a collection or corpus”:
for name, df in reduced_bow.reset_index().groupby('cuisine'):
print(name)
d = df.iloc[:, 1:]
means = d[d > 0].sum(axis=0).dropna()
representative = means[means == max(means)].index
# print the proportion of usage of most representative ingredients in the total of recipes
print(representative[0], (df.loc[:, representative].astype(bool).sum()/df.shape[0])[0], '\n')
brazilian
onions 0.3477088948787062
british
milk 0.2623626373626374
cajun_creole
cajun seasoning 0.19230769230769232
chinese
soy sauce 0.5137067938021455
filipino
soy sauce 0.35235378031383735
french
unsalted butter 0.2300292764533668
greek
feta cheese crumbles 0.22082585278276481
indian
garam masala 0.2680334092634776
irish
butter 0.33766233766233766
italian
olive oil 0.40968138930671405
jamaican
ground allspice 0.24008350730688935
japanese
mirin 0.29049844236760125
korean
sesame oil 0.4879898862199747
mexican
jalapeno chilies 0.17570573139435414
moroccan
ground cumin 0.427972027972028
russian
sour cream 0.2411504424778761
southern_us
all-purpose flour 0.2964635063957863
spanish
olive oil 0.3936750272628135
thai
fish sauce 0.40211267605633805
vietnamese
fish sauce 0.46618705035971225
It makes sense!!. Now we can tackle the classification issue. In this edition of the post I will work with the simplest ML model in my opinion: Naïve Bayes. Since we have multiple classes, let’s try first the Multinomial model. To be able to test the classification we need to split our data into training and testing, and then proceed with the cross-validation:
train, test = train_test_split(reduced_bow, test_size=0.1, stratify=reduced_bow.index)
mnb = MultinomialNB()
mnb_fit = mnb.fit(train, train.index)
pred = mnb.predict(test)
print(metrics.classification_report(test.index.tolist(), pred))
precision recall f1-score support
brazilian 1.00 0.11 0.20 37
british 0.55 0.08 0.14 73
cajun_creole 0.84 0.58 0.69 140
chinese 0.65 0.92 0.76 252
filipino 1.00 0.33 0.49 70
french 0.53 0.41 0.46 239
greek 0.89 0.30 0.45 111
indian 0.76 0.92 0.84 263
irish 0.88 0.11 0.20 62
italian 0.67 0.90 0.77 731
jamaican 1.00 0.29 0.45 48
japanese 0.92 0.59 0.72 128
korean 1.00 0.43 0.60 79
mexican 0.85 0.91 0.88 585
moroccan 0.92 0.46 0.61 72
russian 1.00 0.02 0.04 45
southern_us 0.52 0.83 0.64 399
spanish 1.00 0.12 0.21 92
thai 0.69 0.78 0.74 142
vietnamese 1.00 0.10 0.18 70
accuracy 0.70 3638
macro avg 0.83 0.46 0.50 3638
weighted avg 0.75 0.70 0.66 3638
The class imbalance can be affecting the prediction. Let’s try the more robust (in terms of class imbalance) Complement Naive bayes:
mnb = ComplementNB()
mnb_fit = mnb.fit(train, train.index)
pred = mnb.predict(test)
print(metrics.classification_report(test.index, pred))
precision recall f1-score support
brazilian 0.89 0.43 0.58 37
british 0.46 0.15 0.23 73
cajun_creole 0.76 0.62 0.68 140
chinese 0.67 0.90 0.77 252
filipino 0.82 0.33 0.47 70
french 0.61 0.49 0.54 239
greek 0.77 0.42 0.55 111
indian 0.73 0.94 0.83 263
irish 0.57 0.27 0.37 62
italian 0.76 0.90 0.82 731
jamaican 0.96 0.52 0.68 48
japanese 0.85 0.70 0.77 128
korean 0.97 0.47 0.63 79
mexican 0.85 0.92 0.88 585
moroccan 0.83 0.56 0.67 72
russian 0.75 0.33 0.46 45
southern_us 0.57 0.80 0.67 399
spanish 0.70 0.17 0.28 92
thai 0.65 0.75 0.70 142
vietnamese 0.57 0.06 0.10 70
accuracy 0.73 3638
macro avg 0.74 0.54 0.58 3638
weighted avg 0.73 0.73 0.70 3638
The improvement is only marginal. Let’s retry doing an under-sampling to make sure is not the class imbalance:
from collections import Counter
def undersample(df):
gr = df.reset_index().groupby('cuisine')
c = Counter(df.index)
smallest = c.most_common()[-1][1]
under_sampled = pd.concat(sub_df.sample(sub_df.shape[0]).iloc[:smallest, :] for name, sub_df in gr)
idx = set(df.index).difference(under_sampled.index)
rest = df.loc[idx, :]
under_sampled = under_sampled.set_index('cuisine')
return under_sampled, rest
us, rest = undersample(reduced_bow)
print(us.shape)
us.head()
(7420, 2405)
| tomato paste | tomato sauce | 1% low-fat cottage cheese | 1% low-fat milk | 2% reduced-fat milk | aai | achiote paste | acorn squash | active dry yeast | adobo | ... | yellow split peas | yellow squash | yellow summer squash | yoghurt | yolk | yukon gold potatoes | zesty italian dressing | zinfandel | ziti | zucchini | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| cuisine | |||||||||||||||||||||
| brazilian | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| brazilian | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| brazilian | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| brazilian | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| brazilian | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ... | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
5 rows × 2405 columns
train, test = train_test_split(us.iloc[:,1:], test_size=0.1, stratify=us.index)
mnb = ComplementNB()
mnb_fit = mnb.fit(train, train.index)
pred = mnb.predict(test)
print(metrics.classification_report(test.index, pred))
precision recall f1-score support
brazilian 0.68 0.57 0.62 37
british 0.32 0.35 0.33 37
cajun_creole 0.71 0.78 0.74 37
chinese 0.69 0.73 0.71 37
filipino 0.68 0.51 0.58 37
french 0.48 0.41 0.44 37
greek 0.66 0.84 0.74 37
indian 0.70 0.84 0.77 37
irish 0.54 0.41 0.46 37
italian 0.57 0.62 0.60 37
jamaican 0.82 0.73 0.77 37
japanese 0.77 0.61 0.68 38
korean 0.67 0.81 0.73 37
mexican 0.67 0.89 0.77 37
moroccan 0.66 0.89 0.76 37
russian 0.52 0.46 0.49 37
southern_us 0.55 0.57 0.56 37
spanish 0.75 0.41 0.53 37
thai 0.60 0.71 0.65 38
vietnamese 0.62 0.49 0.55 37
accuracy 0.63 742
macro avg 0.63 0.63 0.62 742
weighted avg 0.63 0.63 0.62 742
We can see now more balance scores, although there is plenty of room for improvement an overall f1-score of 65 is not the sexiest f1-score, but will do for this post. Plase keep an eye open for follow-up posts.
I’ll be happy to get your comments and suggestions!!

